lgamma(), lgamma_r(), lgammaf(), lgammaf_r()

Log gamma function

Synopsis:

#include <math.h>

double lgamma( double x );

double lgamma_r( double x,
                 int* signgamp);

float lgammaf( float x );

float lgammaf_r( float x,
                 int* signgamp);

Arguments:

x

An arbitrary number.

signgam

(lgamma_r(), lgammaf_r() only) A pointer to a location where the function can store the sign of Γ(x).

Library:

libm

Use the -l m option to qcc to link against this library.

Description:

The lgamma() and lgamma_r() functions return the natural log (ln) of the Γ function and are equivalent to gamma(). These functions return ln|Γ(x)|, where Γ(x) is defined as follows:

For x > 0:

For x < 1:

n / (Γ( 1-x ) * sin( nx ))

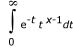
The results converge when x is between 0 and 1. The Γ function has the property:

Γ(N) = Γ(N-1)×N

The lgamma* functions compute the log because the Γ function grows very quickly.

The lgamma() and lgammaf() functions use the external integer signgam to return the sign of Γ(x), while lgamma_r() and lgammaf_r() use the user-allocated space addressed by signgamp.

---

The signgam variable isn't set until lgamma() or lgammaf() returns. For example, don't use the expression: g = signgam * exp( lgamma( x )); to compute g = Γ(x)'. Instead, compute lgamma() first: lg = lgamma(x); g = signgam * exp( lg );

---

Note that Γ(x) must overflow when x is large enough, underflow when -x is large enough, and generate a division by 0 exception at the singularities x a nonpositive integer.

Returns:

ln|Γ(x)|

---

If an error occurs, these functions return 0, but this is also a valid mathematical result. If you want to check for errors, set errno to 0, call the function, and then check errno again. These functions don't change errno if no errors occurred.

---

Examples:

#include <stdio.h>
#include <errno.h>
#include <inttypes.h>
#include <math.h>
#include <fpstatus.h>

int main(int argc, char** argv) 
{
    double a, b;

    errno = EOK;
    a = 0.5;
    b = lgamma(a);
    printf("lgamma(%f) = %f %d \n", a, b, errno);

    return(0);
}

produces the output:

lgamma(0.500000) = 0.572365 0

Classification:

lgamma() and lgammaf() are ANSI, POSIX 1003.1; lgamma_r() and lgammaf_r() are QNX Neutrino

See also:

gamma()